Coloquio centenario RSME 2011  

En 2011 se cumple el centenario de la creación de la  Real Sociedad Matemática Española (RSME). Entre otros actos conmemorativos, se están celebrando una serie de diez  “Coloquios del centenario RSME”  conferencias patrocinadas por la RSME en Facultades e Institutos de Matemáticas repartidos por todo el territorio nacional, impartidas por conferenciantes de prestigio.

En el Coloquio de la Universidad de Extremadura se impartirán dos conferencias, pensadas para que resulten especialmente atractivas para alumnos de Matemáticas y jóvenes investigadores:

Fecha: viernes, 4 de noviembre de2011 a las 11:00 horas.

Lugar: Salón de Actos de la Facultad de Ciencias (Edificio Juan Remón Camacho, antiguo Rectorado)

 

Programa

Conjuntos de anchura constante, por José Pedro Moreno, Universidad Autónoma de Madrid.

 

Un problema de apariencia sencilla, por Carlos Benítez Rodríguez, Universidad de Extremadura.

 

La labor investigadora de estos autores toma el mundo de los espacios de Banach como punto de referencia, para estudiar las propiedades de los conjuntos convexos. Ambos han obtenido resultados publicados en las revistas de mayor nivel y en revistas especializadas de alta calidad.

Resúmenes de las conferencias

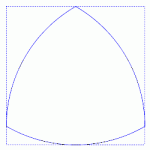
Conjuntos de Anchura constante:

 La anchura de un conjunto convexo en el plano se define como la distancia entre dos líneas paralelas que lo soportan. Si esta anchura no depende de la orientación de las líneas se dice que el conjunto tiene anchura constante. Los ejemplos más sencillos son el círculo (que es el de mayor área) y el triángulo de Reuleaux (el de menor área). Mediante una sencilla generalización se pueden definir cuerpos sólidos (en cualquier dimensión) de anchura constante. 

 

Desde hace poco tiempo la ciudad de Valencia tiene un circuito urbano que es una de las sedes (con polémica incluida) del Mundial de Fórmula 1, pero ¿qué tienen en común el motor del deportivo que aparece en estas fotografías, ganador de muchos grandes premios, y una de las ventanas de la catedral de dicha ciudad?

Las tapas de alcantarilla son peligrosas en las carreras cuando éstas tienen lugar en un trazado urbano. En Mónaco las sueldan cada año para garantizar que los monoplazas no las levantan con el efecto de vacío que provocan a su paso. La pregunta de por qué la mayoría de estas tapas son circulares se hizo famosa cuando Microsoft la incluyó en un cuestionario para contratar personal.  ¿Por qué no son habitualmente de otra forma, por ejemplo cuadradas?  Y puestos a reflexionar sobre la forma de las cosas, otra pregunta en la misma dirección: ¿tienen que ser las monedas necesariamente redondas?

 

 

Sin dejar todavía la cuestión del transporte, es frecuente escuchar o leer que la rueda es el mayor invento de la humanidad, que este asunto va sobre ruedas o que tal cosa es un negocio redondo. Sin embargo, es posible construir vehículos con ruedas que no son circulares:

 

Durante la charla intentaremos responder a estas preguntas, aclarar alguna de estas cuestiones y conocer un poco más los conjuntos de anchura constante, que en el pasado atrajeron la atención de Euler, Lebesgue y otros matemáticos brillantes y que a su innegable belleza son capaces de añadir sorprendentes aplicaciones a la ciencia y la ingeniería.

 

Un problema de apariencia sencilla:

 

El “sencillo» problema es el de ver si siempre se cumple una cierta desigualdad en los espacios vectoriales de dimensión n dotados de un producto escalar,  que es  trivial en dimensión dos. Utilizando técnicas de Análisis Complejo se conocen al menos dos demostraciones de que es cierta cuando el espacio es complejo. Para el caso real el problema permanece abierto desde hace años  y ha merecido la publicación de no menos de veinte artículos. Se conocen, por tanto, bastantes resultados parciales y unas cuantas formulaciones equivalentes, unas de naturaleza puramente algebraica, otras de naturaleza puramente geométrica. Tales formulaciones, fáciles de comprender y manejar, hacen pensar que el problema es bastante más fácil de lo que, en realidad, debe ser. (Debido a ello, bien podríamos decir que estamos ante un “tantalizing problem»).