Tablas
Introducción
La presentación de datos estadísticos se apoya en dos
formatos fundamentales:
- Tablas: Es el procedimiento de presentación mediante el
que la información aparece de forma muy completa y detallada.
Como incoveniente esta información no resulta intuitiva. Si
presentamos tres valores medios, puede ser fácil ver su
ordenación; pero ya no es tan fácil sin hacer cuentas
mentales saber si el valor del centro si se situa más cerca de
uno u otro valor extremo.
- Representaciones gráficas: Es un procedimiento de
presentación más intuitivo, aunque resulta menos
detallado y exacto que el procedimiento anterior. Veremos ejemplos de
ambos.
Tanto las tablas como las gráficas se utilizan para
representar dos formas de resumir la información contenida en
los datos Estadísticos: Frecuencias y Estadísticos.
Open Office presenta una gran capacidad para adaptar el aspecto a
las
necesidades y al gusto estético de cada usuario. No entraremos
en esta cuestión en este tutorial. Dentro del comando Formato->Celdas...
se pueden encontrar las diferentes solapas que permiten conseguir el
aspecto deseado para una tabla. Son bastante autoexplicativas y no
requieren más que algún tiempo de ensayo y uso para
llegar a dominarlas. Además existen otros tutoriales en Internet
que abordan esta cuestión.
Frecuencias
Las frecuencias son el recuento de las veces que aparece en
determinado valor de una variable estadística en un conjunto de
datos. Pueden ser frecuencias relativas o frecuencias absolutas. Las
primeras son el recuento directo del número de repeticiones y el
segundo es el resultado de dividir la frecuencia absoluta por el
número total de datos. Además no es extraño que la
frecuencia relativa aparezca presentada en forma de porcentaje.
En OpenCalc se pueden utilizar dos formas de calcular frecuencias.
La primera es adecuada para cualquier tipo de variables y en realidad
es un ejercicio que ya se hizo en el primer tutorial. La segunda es
específica para variables cuantitativas y es bastante más
potente que la primera.
Variables cualitativas
Utilicemos el archivo analisis_de_datos
incluido con la suite parcialmente libre StarOffice 6.0 y de la que procede
el actual proyecto OpenOffice. Es un archivo elaborado por Peter
Thielmann y modificado por Tom Verbeek. Contiene 392 datos
(¿ficticios?)
sobre ventas de productos teléfonicos a 12 clientes ubicados en
diferentes ciudades a lo largo de 26 años.
- Abramos el archivo y situémonos en la casilla C395.
La casilla B395 señala el nombre Alicante.
Trataremos de que en la casilla B395 aparezca la
frecuencia con la Alicante ha realizado ventas, es decir, el
número de años en los que Alicante refleja ventas.
- Pulsemos sobre el botón del asistente de funciones
 para introducir una fórmula.
para introducir una fórmula.
- Elegiremos la función
CONTAR.SI dentro de la
categoría Matemáticas.
- Señalaremos el área b2:b392 como el
lugar donde queremos que cuente el número de veces que aparece Alicante.
Como lo repetiremos posteriormente para las demás ciudades,
utilizaremos referencia absoluta al indicar el número de fila: b2:b392.
- El criterio debería ser
"=Alicante". Podemos
probarlo. Pero esto nos obligaría a utilizar un función
nueva con nombre de ciudad. De modo que dejaremos la expresión
"=" y la reuniremos con el texto de la casilla b395. El
operador para unir textos es &.
Viene a ser con los textos un
operador análogo al operador +
con los números. La pantalla del asistente para funciones debe
quedar así:
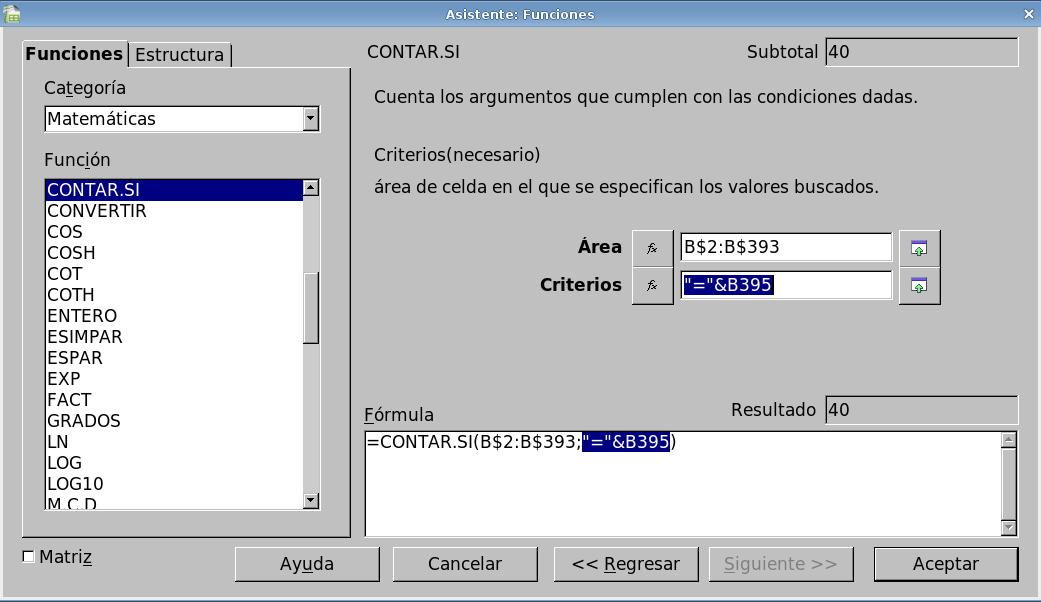
- Extenderemos la función a todas las casillas desde la
celda C395 hasta la C406.
- En la celda C407 pegaremos la función suma
mediante el botón suma ().
- Nos situaremos nuevamente en la celda C407 para
cambiar de lugar la ubicación de la suma mediante las teclas May+Supr
o bien mediante el comando Editar->Cortar.
- Pegaremos en la celda C408 la suma bien mediante
las teclas May+Insert o bien mediante el comando Editar->Pegar.
- En la celda D395 escribiremos la
fórmula =C395/C$395 que nos permitirá
calcular la frecuencia relativa. Utilizaremos una referencia absoluta
para el denominador a fin de poder extender la fórmula a todo el
conjunto de frecuencias.
- Extenderemos la fórmula desde D395 hasta D406
como ya se ha hecho anteriormente.
- Extenderemos la suma de C408 a D408 .
La suma de las frecuencias relativas es siempre la unidad.
- Podemos presentar las frecuencias relativas como porcentajes
seleccionando el área D395:D408 y pulsando el
botón de porcentaje (
 ) nos quedará en la forma
deseada.
) nos quedará en la forma
deseada.
- Finalmente guardemos el archivo tal y como ha quedado pasa uso
futuro.
Variables
cuantitativas
Para las variables cuantitativas se dispone de otra función
algo más versatil que la utilizada para las variables
cualitativas. El cálculo de frecuencias en variables
cuantitativas incluye conceptos algo más sutiles que en el caso
de las variables cualitativas. Especialmente en el caso de variables
que además de ser cualitativas son contínuas es un
cálculo ligado a la idea de intervalo. En las variables
continuas, la frecuencia de un valor de una
variable continua puede no ser representativa de su abundancia en la
población de la que procede nuestra muestra, especialmente si el
número de valores posible de la variable es muy elevado frente
al número de datos disponibles. En estos casos los valores se
agrupan en conjuntos conexos de valores denominados intervalos.
Volvamos a utilizar los datos de Fisher que utilizamos en el
ejercicio
de introducción de datos para ejercitar la construcción
de intervalos para el cálculo de frecuencias en variables
continuas. Los datos completos se encuentran en el archivo iris2.odt.
- Situémonos en la celda A153. Escribamos la
fórmula =MÍN(A2:A151) o bien utilicemos el
asistente para fórmulas elegiéndo la función
MÍN
en la categoría Estadística. Obtendremos el
valor mínimo de las longitudes de los sépalos medidos a
los iris.
- En la celda A154. Escribamos la fórmula =MÁX(A2:A151)
o bien utilicemos el asistente para fórmulas elegiéndo la
función
MÁX en la categoría Estadística.
Obtendremos el valor máximo de las longitudes de los
sépalos medidos a los iris.
- En la celda A156 escribamos 4.
- En la celda A157 escribamos =A156+1.
- Extendamos la fórmula de A157 hasta A160.
- En la celda B163 iniciamos el asistente para
funciones
 y elegimos la función
y elegimos la función FRECUENCIA dentro de la
categoría Matriz. Esta categoría incluye a
las funciones paras las que el resultado no es un único valor,
sino un conjunto de valores, como son por ejemplo: la matriz inversa de
una matriz, la matriz producto de dos matrices, la matriz transpuesta
de una matriz, los parámetros de una regresión lineal, o
en nuestro caso el conjunto de frecuencias asociadas a un conjunto de
intervalos.
- Como datos designaremos el conjunto de valores de las longitudes
de los sépalos: a2:a151.
- El campo grupos designa
los valores de los extremos de los intervalos en los que se desea
agrupar los valores. En nuestro caso los extremos de los intervalos los
hemos puesto en las casillas del rango a156:a160.
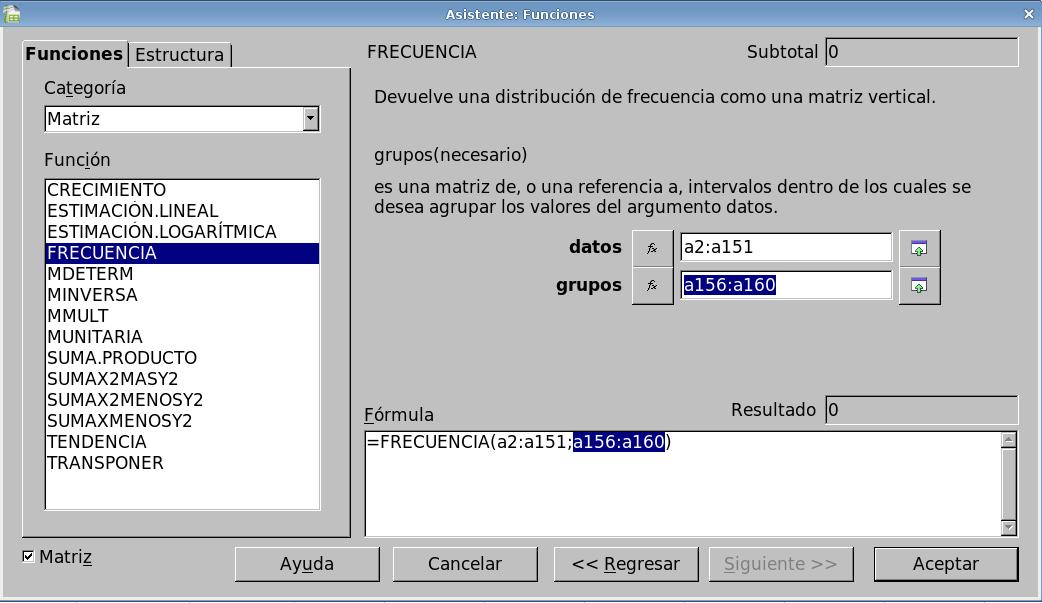
- La ventana del asistente de funciones debe quedar como en la
imagen. No se debe ovildar marcar la casilla Matriz de la esquina
inferior izquierda que nos ahorrará tener que calcular las
frecuencias para cada intervalo como tuvimos que hacerlo en el caso de
las variables cualitativas.
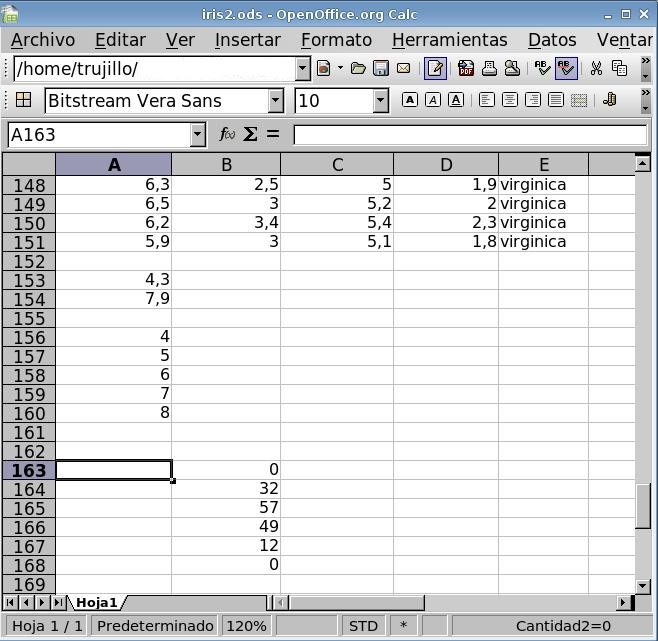
- Cuando pulsemos Aceptar nos quedará la hoja de
cálculo como en la imagen. A partir de los cinco límites
que le hemos propuesto nos ha proporcionado las frecuencias de seis
intervalos. La primera frecuencia es el número de datos para los
que la longitud del sépalo es inferior a cuatro
milímetros. Tal como podemos deducir del valor mínimo del
conjunto de datos, este número ha de ser cero. La última
frecuencia es el número de datos para los que la longitud del
sépalo es superior ocho milímetros. También esta
frecuencia es cero. Otro problema que tenemos es que no sabemos si los
valores 5 pertenecen al primer conjunto o al segundo de frecuencias.
Podemos averiguarlo cambiando el valor 5 por 4.95 y comprobamos que la
frecuencia disminuye pasando de 32 a 22; debemos concluir que hay diez
sepálos cuya longitud es 5 mm. y que están incluidos en
el primer grupo de frecuencias no nulas. A la vista de todo ello vamos
repetir el procedimiento de forma que nos quede todo más claro.
- Mediante las teclas Ctrl+Z. o mediante el
comando Editar->Deshacer. quitamos las frecuencias
que hemos introducido.
- En la celda A156 cambiamos el 4 por el
valor 3,95. Todos los valores cambian de modo que no
tendremos dudas sobre la pertenencia de ningún valor a
algún intervalo, ya que no existen valor con precisión de
centésimas.
- En la celda B163 repetimos el asistente de
funciones, pero esta vez le damos al campo grupos el rango a157:a159,
de este modo evitamos los valores cero de los extremos.
- En la celda B167 calculamos la suma con el
botón suma (
 ) y comprobamos que efectivamente se han
contabilizado todos los datos. Trasladamos esta suma a la celda B168
con las teclas May+Supr y May+Inst como
ya hemos hecho anteriormente.
) y comprobamos que efectivamente se han
contabilizado todos los datos. Trasladamos esta suma a la celda B168
con las teclas May+Supr y May+Inst como
ya hemos hecho anteriormente.
- En la celda A163 calculamos el valor medio o marca
del clase del intervalo al que corresponde la frecuencia de la celda B163.
Introducimos la fórmula: =(A157+A156)/2.
- Extendemos esta fórmula a las casillas del rango A164:A166.
- En la columna C podríamos calcular las
frecuencias relativas como hicimos con la variable cualitativa. En
lugar de utilizar las marcas de clase de los intervalos
podríamos haber puesto en la columna A el inicio
de cada intervalo y en la columna B el final, pero la
disposición actual permite de forma inmediata la
construcción de un diagrama similar a un histograma como veremos
en la sección correspondiente.
Estadísticos
La segunda forma mediante la que podemos resumir la
información contenida en un conjunto de datos es mediante la
utilización de Estadísticos. Dependiendo del tipo de
información que se refleja en el estadístico utilizado
disponemos de tres tipos de Estadísticos. Se volverán a
ver utilizando para ello el R-Commander.
- Estadísticos de posición: Indican en que valores de
la variable podemos encontrar datos. Se les puede clasificar a su vez
en dos tipos:
- Centrales o de centralización: Indican los valores
centrales del conjunto de datos. El más importante es la media.
- No centrales: Indican otros valores en los que podemos
encontrar
datos, pero no son los valores centrales del conjunto de datos.
- Dispersión: Indican como de cerca o de lejos están
los datos entre sí.
- Forma indican si los datos son más abundates en los
valores bajos de la variable o en los valores altos, o en los valores
centrales. A su vez son de dos tipos: Asimetría y Curtosis.
Debido a su mayor complejidad en la interpretación de estos
valores no los estudiaremos en esta parte del curso. Aunque son faciles
de calcular mediante OpenCalc, no son tan fáciles de interpretar
sin disponer de un buen formulario auxiliar.
Utilizaremos de nuevo los datos de Fisher que se encuentran en el
archivo iris2.odt.
Estadísticos
de posición
- Una vez abierto el archivo marcaremos la primera columna pinchando con el ratón en la
cabecera de la misma (donde está la letra
A
mayúscula).
- Mediante el comando Insertar->Columnas
insertaremos una nueva columna a la izquierda de los datos.
(También es posible utilizar el menú contextual que
aparece al pulsar con el botón derecho del ratón en la
cabecera de la columna seleccionada)
- En la celda A153 Escribiremos: Media.
- En la celda B153 bien directamente o bien
mediante el asistente para funciones (
 )
escribiremos la fórmula =promedio(b2:b151). la
función se encuentra en la categoría
)
escribiremos la fórmula =promedio(b2:b151). la
función se encuentra en la categoría Estadística.
- En la celda A154 Escribiremos: Mediana.
- En la celda B154 bien directamente o bien
mediante el asistente para funciones (
 )
escribiremos la fórmula =mediana(b2:b151). la
función se encuentra en la categoría
)
escribiremos la fórmula =mediana(b2:b151). la
función se encuentra en la categoría Estadística.
- En la celda A155 Escribiremos: Moda.
- En la celda B155 bien directamente o bien
mediante el asistente para funciones (
 )
escribiremos la fórmula =moda(b2:b151). la
función se encuentra en la categoría
)
escribiremos la fórmula =moda(b2:b151). la
función se encuentra en la categoría Estadística.
(La moda en las variables continuas como las que nos ocupan no
debería ser calculada directamente como estamos haciendo, sino
que previamente se deberían construir intervalos para garantizar
su representatividad).
- En la celda A156 Escribiremos: Mínimo.
- En la celda A157 Escribiremos: Cuartil
inferior.
- En la celda A158 Escribiremos: Mediana.
- En la celda A159 Escribiremos: Cuartil
superior.
- En la celda A160 Escribiremos: Máximo.
- En la celda H156 Escribiremos: 0.
- En la celda H157 Escribiremos: =h156+1.
- Extenderemos la fórmula de la celda H157
hasta la celda H160.
- En la celda B156 Mediante el asistenten de
funciones (
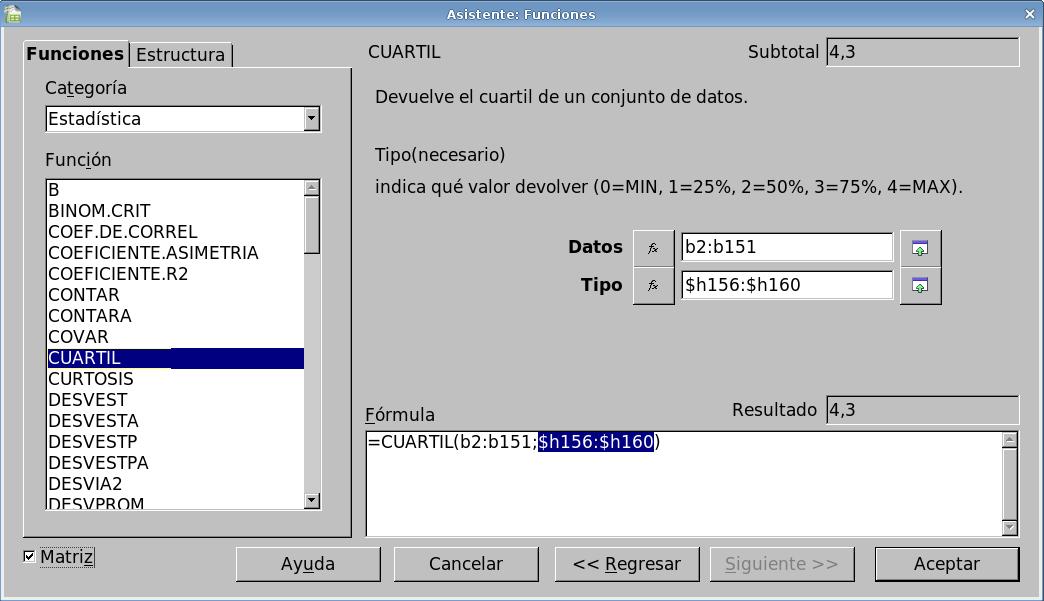
 ) escribiremos la fórmula =cuartil(b2:b151;$h156:$h160).
La ventana del asistente debe quedar como en la siguiente imagen. Una
vez más se debe marcar la casilla matriz
de la esquina inferior izquierda de la ventana.
) escribiremos la fórmula =cuartil(b2:b151;$h156:$h160).
La ventana del asistente debe quedar como en la siguiente imagen. Una
vez más se debe marcar la casilla matriz
de la esquina inferior izquierda de la ventana.
- En la celda A161 Escribiremos: Percentil 10.
- En la celda A162 Escribiremos: Percentil 90.
- En la celda H161 Escribiremos: 0,1.
- En la celda H162 Escribiremos: 0,9.
- En la celda B161 Mediante el asistenten de
funciones (
 ) escribiremos la fórmula =percentil(b2:b151;$h161:$h162).
Una
vez más se debe marcar la casilla matriz
de la esquina inferior izquierda la ventana.
) escribiremos la fórmula =percentil(b2:b151;$h161:$h162).
Una
vez más se debe marcar la casilla matriz
de la esquina inferior izquierda la ventana.
Estadísticos
de dispersión
- En la celda A163 Escribiremos: Varianza.
- En la celda A164 Escribiremos: Desviación
Típica.
- En la celda B163 bien directamente o bien
mediante el asistente para funciones (
 )
escribiremos la fórmula =var(b2:b151). la
función se encuentra en la categoría
)
escribiremos la fórmula =var(b2:b151). la
función se encuentra en la categoría Estadística.
- En la celda B164 bien directamente o bien
mediante el asistente para funciones (
 )
escribiremos la fórmula =desvest(b2:b151). la
función se encuentra en la categoría
)
escribiremos la fórmula =desvest(b2:b151). la
función se encuentra en la categoría Estadística.
Existen dos funciones para el cálculo de la varianza y de
la desviación típica. Cuando se utiliza un conjunto de
datos que debe ser considerado una población en sí mismo,
con todos sus posibles valores, la funciones anteriores deben ser
sustituidas por varp y desvestp
respectivamente. Las funciones
aquí utilizadas son adecuadas para una muestra extraida de una
población; en el denominador de estas función se utilizan
la expresión n-1. Cuando se dispone de una muestra
y se utiliza
el número total de datos n en el denominador el
valor obtenido
tiende a subestimar el verdadero valor poblacional de la varianza y de
la desviación típica.
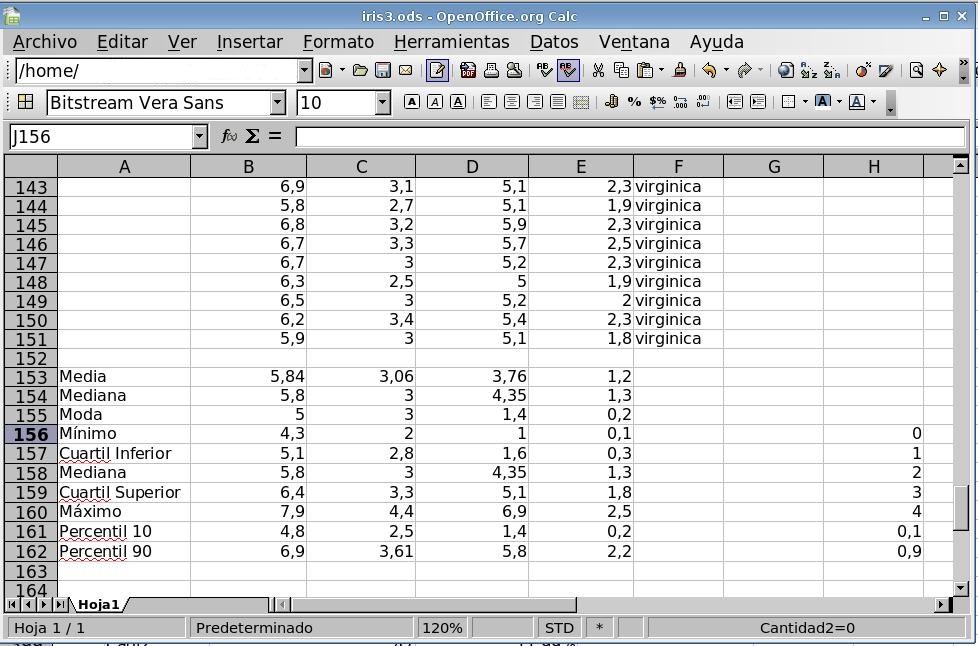
- Terminaremos este ejercicio extendiendo los resultados obtenidos
a las columnas C, D y E
mediante los procedimientos ya vistos. La ventana debe quedar como en
la imagen:
Ejercicio: Media
versus Mediana
Terminemos este capítulo con un ejercicio para poner de
manifiesto las diferentes propiedades de la media y la mediana al
indicar cuales son los valores medios de un conjunto de datos. Puesto
que necesitaremos utilizar pocos datos, utilicemos una hoja de
cálculo nueva. Los datos son los siguientes:
Don
Vito Islero ha abierto una pequeña sucursal de
su negocio (no se entienda para nada tapadera)
para que su hijo vaya aprendiendo. Ha contratado a tres repartidores, un capataz que los coordine y subyugue
adecuadamente, un encargado
que sepa escribir (no creyó necesario que el capataz sepa
escribir) y se encargue de
recoger los pedidos y un administrativo
que mantenga las diversas cuentas que necesitará; finalmente
y por supuesto el hijo es el gerente.
Los sueldos asignados han sido 300€ para los que se la juegan en las
motos, 450€ para el capataz que los mantiene a raya, 750€ para el
encargado de que todo parezca que funciona y 900€ para el
administrativo-blanqueador (no lo encontró más barato
capaz de blanquear bien las cuentas). Para asegurarse la
recuperación de las no-inversiones y que el chaval tenga para
sus gastos, al hijo-gerente se le asigna un sueldo mensual de 6 000€.
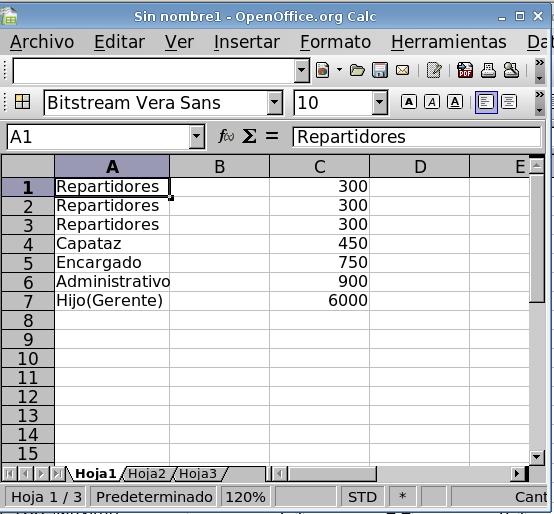
- A partir de la casilla A1 Iremos poniendo los datos
en dos columnas hasta que queden como en la imagen:
- En la celda C8 calcularemos la suma (botón
 )
de los sueldos mensuales y mediante los comandos Editar->Cortar
(May+Supr) y Editar->Pegar. (May+Insert)
la trasladaremos a la celda C9.
)
de los sueldos mensuales y mediante los comandos Editar->Cortar
(May+Supr) y Editar->Pegar. (May+Insert)
la trasladaremos a la celda C9.
- En las celdas C10 y C11 calcularemos
la media y la mediana como hicimos en el ejercicio anterior.
- En las celdas B9, B10 y B11
colocaremos los textos Suma, Media y Mediana.
El resultado debe quedar como en la imagen:
- Seleccionando todo el rango C1:C11 lo convertiremos
al formato moneda (
 ) para que sea más legible. El
resultado debeería quedar como en la figura:
) para que sea más legible. El
resultado debeería quedar como en la figura:
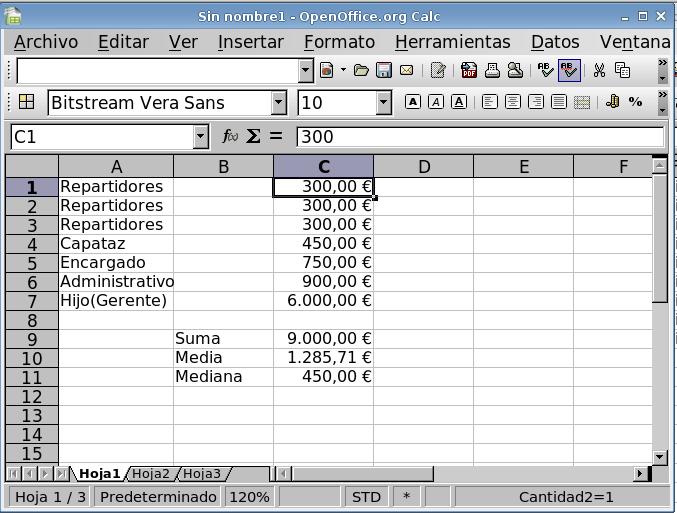
En este exagerado ejemplo la mitad de los valores son
inferiores a la mediana y la mitad superiores, por definición de
mediana. En cambio solo un valor supera a la media. Las distribuciones
de los datos en los que la media se situa en las proximidades de la
mediana y hay una única moda que también está en
las proximidades de la media y la mediana, son simétricas
(pueden
pasar cosas muy diversas cuando aparece la multimodalidad,
varias modas). Por el contrario cuando abundan los datos menores que la
media y escasean los datos superiores a la media o viceversa se habla
de distribuciones asimétricas. El caso que nos ocupa se denomina
asimetría positiva y es muy frecuente en muchos tipos de
variables, entre otros en las variables económicas. Es poco
habitual la presentación de la mediana; cuando aparece es
común verla con el nombre de percentil 50. No es
raro encontrar en ocasiones que el percentil 50 llega a ser casi la
mitad de la media en disponibilidad de renta por ejemplo.
 para introducir una fórmula.
para introducir una fórmula.
 ) nos quedará en la forma
deseada.
) nos quedará en la forma
deseada.

 ) y comprobamos que efectivamente se han
contabilizado todos los datos. Trasladamos esta suma a la celda B168
con las teclas May+Supr y May+Inst como
ya hemos hecho anteriormente.
) y comprobamos que efectivamente se han
contabilizado todos los datos. Trasladamos esta suma a la celda B168
con las teclas May+Supr y May+Inst como
ya hemos hecho anteriormente.


 ) para que sea más legible. El
resultado debeería quedar como en la figura:
) para que sea más legible. El
resultado debeería quedar como en la figura: